Modern Cryptography, Part II - Rise of Quantum Computers Pose Threat to Data Safety
Quantum computers are set to break the encryption protecting today’s digital world. The previous part explained how current cryptography works and in this blog we'll know why quantum computing threatens it, and how quantum-resistant algorithms like Kyber and Dilithium are shaping the future of secure communication. A simple, clear guide to the next big shift in cybersecurity.

Understanding the Quantum Threat
What is a Quantum Computer?

Traditional computers operate using bits i.e binary states representing 0 or 1. Quantum computers leverage qubits (quantum bits), which exploit quantum mechanical properties to exist in superposition: a probabilistic combination of both 0 and 1 states simultaneously until measurement occurs.
To understand this conceptually, consider a classical bit as analogous to a coin resting on a table—definitively heads (1) or tails (0). A qubit is better compared to a coin spinning in mid-air, simultaneously representing both states until it lands and collapses to a definite value.
Additionally, qubits can be entangled—a quantum phenomenon where the state of one qubit becomes correlated with another, regardless of spatial separation. When one entangled qubit is measured, the state of its partner is instantaneously determined.
These properties enable quantum computers to evaluate multiple computational paths in parallel, providing exponential speedup for specific problem classes, particularly those involving number theory and unstructured search.
The RSA and ECC Vulnerability: Shor's Algorithm
In 1994, mathematician Peter Shor developed a quantum algorithm that fundamentally undermines the security assumptions of modern public-key cryptography. Shor's algorithm efficiently solves two computationally hard problems:
- Integer factorization — breaks RSA encryption
- Discrete logarithm computation — breaks ECC and Diffie-Hellman key exchange
Both operations execute in polynomial time on a quantum computer, a dramatic departure from the exponential complexity required by classical algorithms.
Comparative Computational Complexity

Classical Computing:
- Factoring a 2048-bit RSA modulus: ~1020 operations (infeasible with current resources)
- Computing discrete logarithms for 256-bit ECC: Similar complexity class
Quantum Computing with Shor's Algorithm:
- Factoring RSA-2048: Achievable in hours to weeks with sufficient qubits
- Computing ECC-256 discrete logs: Similar timeframe
This represents not incremental improvement but a fundamental complexity class reduction—from intractable to practical.
The Timeline Has Accelerated
Early estimates suggested breaking RSA-2048 would require approximately 20 million physical qubits. However, research published in May 2025 by Google researcher Craig Gidney demonstrates that optimized quantum circuits can achieve RSA-2048 factorization with fewer than one million qubits in under one week—a 20-fold reduction in hardware requirements.

This is significant because quantum computing capabilities are advancing rapidly:
-
IBM's quantum roadmap indicates systems exceeding 1,000 qubits deployed in 2025–2026.
-
Google's Willow chip (105 qubits, December 2024) demonstrated exponential error suppression—a critical milestone for quantum error correction.
-
Microsoft's Majorana 1 chip (8 topological qubits, early 2025) introduces a new topoconductor material and topological architecture with a roadmap to scale to 1 million physical qubits on a single chip, leveraging inherent error resistance.
-
Multiple vendors have published roadmaps targeting million-qubit systems within the next decade.
-
Current generation quantum computers have surpassed 1,000 qubits (IBM Condor, IBM Heron systems).
We are transitioning from theoretical threat to practical timeline. RSA-breaking quantum computers may emerge by 2030—potentially sooner with continued algorithmic optimization.
Security Implications
An adversary with access to a cryptographically relevant quantum computer (CRQC) can:
1. Forge TLS Certificates
Recover a Certificate Authority's private signing key, enabling impersonation of arbitrary websites through fraudulent certificate issuance.
2. Compromise Digital Identities
Extract users' private keys from captured authentication traffic, allowing signature forgery and identity theft.
3. Decrypt Historical Communications
Apply Shor's algorithm to intercepted Elliptic Curve Diffie-Hellman (ECDH) key exchanges, recovering session keys and decrypting all past encrypted sessions.
This last capability is the most concerning from a threat modeling perspective.
Grover's Algorithm: Impact on Symmetric Cryptography
Grover's algorithm provides quantum computers with quadratic speedup for unstructured search problems, affecting symmetric encryption and cryptographic hash functions.
Security Reduction
Classical Brute Force:
- Breaking AES-256: Requires ~2255 operations on average (computationally infeasible)
Quantum Attack with Grover's Algorithm:
- Breaking AES-256: Reduces to ~2128 operations (equivalent to classical AES-128 security)
Practical Mitigation
The impact on symmetric cryptography is manageable:
- AES-256 maintains adequate security against quantum attacks (effective 128-bit security)
- AES-128 becomes potentially vulnerable (reduced to 64-bit effective security)
Recommendation: Standardize on AES-256 for all new implementations. Most production systems already meet this requirement.
Unlike asymmetric cryptography, symmetric algorithms do not face existential threats from quantum computing—only a quantifiable security margin reduction that can be addressed through increased key sizes.
Harvest Now, Decrypt Later: The Active Threat
The most operationally significant attack vector is not hypothetical—it is occurring at scale today.
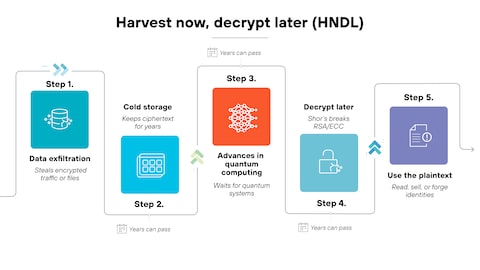
Attack Timeline and Methodology
Current State (2025):
Nation-state adversaries and sophisticated threat actors are conducting large-scale collection of encrypted traffic:
- TLS/HTTPS sessions from backbone intercepts
- Encrypted email archives (S/MIME, PGP)
- VPN tunnel captures
- Classified government communications
- Corporate trade secret transmissions
- Healthcare data in transit
Current quantum computers have surpassed 1,000 qubits (IBM systems, Google's Willow chip), but they remain too noisy. Quantum decoherence and error rates prevent practical execution of Shor's algorithm at scale. However, error correction techniques are improving exponentially.
Projected Capability Window (2030-2035):
Quantum computers with approximately one million error-corrected qubits become operational, capable of executing Shor's algorithm against RSA-2048 in under a week. Adversaries retroactively decrypt stored communications by:
- Extracting ephemeral ECDH public keys from captured TLS handshakes
- Computing discrete logarithms via Shor's algorithm to recover private keys
- Reconstructing session keys used for symmetric encryption
- Decrypting all historical traffic encrypted under those session keys
Impact Assessment
Compromised Data Categories:
- Medical records revealing sensitive health information
- Attorney-client privileged communications
- Merger and acquisition negotiations
- Government classified intelligence
- Proprietary research and development data
- Authentication credentials and secrets
Risk Classification by Data Sensitivity Period
5 years or less: Moderate risk (quantum capabilities may not reach threshold)
5-10 years: Elevated risk (migration planning should be underway)
10+ years: Critical risk—post-quantum cryptography (PQC) deployment is urgent
Examples requiring long-term confidentiality:
- Healthcare records (regulatory retention requirements plus lifetime medical history)
- Legal documents with attorney-client privilege
- Government classified material with multi-decade classification periods
- Pharmaceutical research and clinical trial data (patent lifecycle protection)
- Corporate strategic plans, M&A communications, and trade secrets
- Intellectual property and patent applications
Any data encrypted today with RSA or ECC that requires confidentiality beyond 2030-2035 is at risk. The cryptographic protection is effective now, but the adversary only needs to wait—and the wait time is shortening faster than previously anticipated.
Post-Quantum Cryptography: Defensive Countermeasures
Why Not Immediate Full Deployment?
Several operational constraints prevent immediate wholesale replacement of existing cryptographic infrastructure:
- Backward compatibility: Legacy systems lack PQC algorithm support
- Implementation maturity: New algorithms require extensive real-world validation
- Cryptanalytic uncertainty: Novel algorithms may contain undiscovered vulnerabilities
- Risk management: Hybrid approaches provide defense-in-depth
The Hybrid Cryptographic Strategy
Current best practice combines classical and post-quantum algorithms in a hybrid construction, providing protection against both classical and quantum adversaries.
TLS 1.3 Hybrid Key Exchange Example:
1. Algorithm Negotiation:
- Classical: ECDH using Curve25519 or P-256
- Post-Quantum: ML-KEM (Kyber) at appropriate security level
2. Classical Key Agreement:
- Perform ECDH ephemeral key exchange
- Derive: shared_secret_ecdh
3. Post-Quantum Key Encapsulation:
- Execute ML-KEM encapsulation mechanism
- Derive: shared_secret_pqc
4. Key Combination:
- Compute: master_secret = KDF(shared_secret_ecdh || shared_secret_pqc || handshake_context)
( || denotes concatenation )
5. Session Key Derivation:
- Generate AES-256-GCM keys from master_secret using HKDF
Security Properties:
- If ML-KEM is cryptanalyzed: ECDH provides security against classical attacks.
- If quantum computers break ECDH: ML-KEM maintains confidentiality.
- Defense-in-depth against unknown vulnerabilities in either construction.
This approach maximizes security with current knowledge while hedging against both implementation flaws and cryptanalytic breakthroughs.
NIST Post-Quantum Cryptography Standards
Following a six-year public competition and extensive cryptanalytic review, NIST published final post-quantum cryptographic standards in August 2024.
ML-KEM (Module Lattice Key Encapsulation Mechanism)
Standard: FIPS 203
Purpose: Replace ECDH for key establishment in TLS, VPNs, and secure channels
Cryptographic Foundation:
ML-KEM's security is based on the Module Learning With Errors (Module-LWE) problem. A lattice-based hard problem. The construction involves:
- Key Generation:
- Generate random matrix A ∈ R^(k×k) where R is a polynomial ring
- Sample secret vectors s, e from discrete Gaussian distributions
- Compute public key: t = A · s + e
- Public key = (A, t); Secret key = s
- Encapsulation (Sender):
- Sample random r, e₁, e₂ from error distributions
- Compute ciphertext components:
- u = Aᵀ · r + e₁
- v = tᵀ · r + e₂ + Encode(message)
- Shared secret derived from message via KDF
- Transmit (u, v)
- Decapsulation (Receiver):
- Recover: v - sᵀ · u ≈ Encode(message)
- The structured noise ensures only the legitimate recipient with s can decode
- Derive shared secret from recovered message
Quantum Resistance:
Shor's algorithm provides no advantage against lattice problems. Grover's algorithm offers only square-root speedup, which is mitigated by parameter selection.
Parameter Sets and Security Levels:
- ML-KEM-512: 128-bit quantum security (equivalent to AES-128)
- ML-KEM-768: 192-bit quantum security (equivalent to AES-192)
- ML-KEM-1024: 256-bit quantum security (equivalent to AES-256)
Performance Characteristics:
- Public key: 800-1,568 bytes (depending on security level)
- Ciphertext: 768-1,088 bytes
- Computational overhead: Moderate (typically 2-5ms per operation on modern hardware)
Size increase versus ECDH (~65 bytes) is manageable for modern network infrastructure.
ML-DSA (Module Lattice Digital Signature Algorithm)
Standard: FIPS 204
Purpose: Replace ECDSA/RSA for certificate signing, code signing, and document authentication
Cryptographic Construction:
- Key Generation:
- Generate public matrix A ∈ R^(k×ℓ)
- Sample secret vectors s₁ ∈ R^ℓ, s₂ ∈ R^k from discrete distributions
- Compute t = A · s₁ + s₂
- Public key: (A, t); Secret key: (s₁, s₂)
- Signing:
- Hash message to produce challenge polynomial
- Generate random masking vector y
- Compute w = A · y
- Calculate challenge c = H(w, message)
- Compute signature components: z = y + c · s₁
- Apply rejection sampling: if ||z|| exceeds bound, restart with new y
- Output signature: (z, c, hint)
- Verification:
- Recompute w' from z, c, public key, and hint
- Hash w' with message to get c'
- Accept if c' = c and ||z|| within bounds
Quantum Resistance:
Based on Module-LWE; no known quantum advantage beyond Grover's speedup.
Signature Sizes:
- ML-DSA-44: ~2,420 bytes (128-bit security)
- ML-DSA-65: ~3,309 bytes (192-bit security)
- ML-DSA-87: ~4,627 bytes (256-bit security)
Larger than ECDSA (64 bytes) but smaller than RSA-2048 signatures (256 bytes). Acceptable overhead for certificate chains and signed artifacts.
SLH-DSA (Stateless Hash-Based Digital Signature Algorithm)
Standard: FIPS 205
Purpose: Conservative signature scheme for long-term archives, legal documents, and high-assurance applications
Design Philosophy:
SLH-DSA (SPHINCS+) is based exclusively on cryptographic hash functions, avoiding new mathematical assumptions. Security reduces directly to hash function collision and preimage resistance.
Conceptual Structure:
SPHINCS+ constructs a hypertree—a tree of Merkle trees:
- Base layer: Multiple WOTS+ (Winternitz One-Time Signature) keys
- Authentication paths: Merkle trees provide authentication from leaf to root
- Hypertree structure: Multiple layers of trees for scalability
- Root: Public key
Signing Process:
- Deterministically select which WOTS+ key to use based on message hash
- Generate one-time signature with selected key
- Provide Merkle authentication path from leaf to root
- Include hypertree authentication across layers
Verification:
- Verify one-time signature
- Recompute Merkle path to root
- Check root matches public key
Trade-offs:
- Public key: 32-64 bytes (compact)
- Signature size: ~7,856-49,856 bytes depending on parameters (substantial)
- Security assumption: Minimal—relies only on hash function security
- Performance: Slower than lattice-based schemes
Use Cases:
Ideal for applications requiring maximum confidence over decades:
- Government document archives
- Legal records and contracts
- Patent filings
- Long-term timestamping authorities
- Situations where signature verification happens infrequently
Algorithm Comparison Matrix
| Property | ML-KEM | ML-DSA | SLH-DSA |
|---|---|---|---|
| Application | Key encapsulation | Digital signatures | Digital signatures |
| Classical threat | None | RSA/ECDSA broken | RSA/ECDSA broken |
| Quantum threat | Shor's algorithm | Shor's algorithm | Shor's algorithm |
| Security basis | Module-LWE (lattice) | Module-LWE (lattice) | Hash functions only |
| Public key | 800-1,568 bytes | 1,312-2,592 bytes | 32-64 bytes |
| Signature/CT | 768-1,088 bytes | 2,420-4,627 bytes | 7,856-49,856 bytes |
| Performance | Moderate | Moderate | Slower |
| Standardization | FIPS 203 (2024) | FIPS 204 (2024) | FIPS 205 (2024) |
| Maturity | Well-studied | Well-studied | Conservative choice |
Quantum Key Distribution (QKD): Physics-Based Security
QKD represents a fundamentally different approach—leveraging quantum mechanical properties rather than computational hardness assumptions.
Core Principle
QKD exploits the quantum no-cloning theorem and measurement disturbance: any attempt to intercept and measure quantum states introduces detectable noise. This enables provably secure key distribution assuming:
- Quantum mechanics are correct (well-established).
- Authenticated classical channel exists (requires separate authentication).
- Single-photon sources and detectors function correctly.
BB84 Protocol
The foundational QKD protocol, proposed by Bennett and Brassard in 1984.
Encoding Bases:

- Rectilinear basis: {|0⟩, |1⟩} --- photon polarization at 0° or 90°
- Diagonal basis: {|+⟩, |−⟩} --- photon polarization at 45° or 135°
Protocol Execution:
- Quantum Transmission:
- Alice randomly selects basis (rectilinear or diagonal) for each bit
- Alice encodes bit value in chosen basis
- Alice transmits single photon with corresponding polarization state
- Bob randomly selects measurement basis for each photon
- Bob measures arriving photon, obtaining classical bit result
- Basis Reconciliation (Classical Channel):
- Alice and Bob publicly compare basis choices (not bit values)
- They retain only bits where bases matched (~50% of transmitted photons)
- Result: "sifted key" of length n/2 from n photons transmitted
- Eavesdropping Detection:
- Alice and Bob publicly compare random subset of sifted key bits
- No eavesdropper: Error rate ≈ 0% (only noise from channel)
- Eavesdropper present: Error rate ≈ 25% (Eve's incorrect basis measurements introduce detectable disturbance)
- If error rate exceeds threshold (typically 11%), abort and restart
- Privacy Amplification:
- Apply information-theoretic secure key distillation
- Extract shorter key guaranteed secure against partial information leakage
Security Analysis:
An eavesdropper (Eve) attempting interception:
- Must measure each photon (no-cloning theorem prevents copying)
- Chooses wrong basis 50% of the time
- Wrong basis measurement yields random result (50% error)
- Remitted photon to Bob carries disturbed state
- Bob's measurement reveals error ~25% of the time overall
- Error rate statistically distinguishes eavesdropping from channel noise
Practical QKD Limitations
Distance Constraints:
- Single-photon QKD: 100-300 km via optical fiber without repeaters
- Advanced protocols (decoy states, twin-field): 500-1,000 km
- Satellite-based QKD: Ground-to-satellite demonstrated (China's Micius)
Infrastructure Requirements:
- Dedicated optical fiber or free-space quantum channel
- Single-photon sources (attenuated lasers or quantum dots)
- Single-photon detectors (superconducting nanowire detectors, avalanche photodiodes)
- Specialized quantum optics equipment (costly compared to classical routers)
Performance:
- Key generation rate: ~1 Mbps in modern systems (sufficient for periodic key refresh, not bulk encryption)
- Higher loss rates at longer distances reduce throughput
Authentication Problem:
- QKD distributes keys but provides no authentication
- Classical authentication (digital signatures) required to prevent man-in-the-middle attacks
- Creates circular dependency: need authenticated channel to bootstrap QKD
Operational Model:
- Point-to-point links only (no transparent network routing)
- Requires trusted nodes for network extension
- Best suited for fixed infrastructure (data center interconnects, government networks)
Current QKD Deployments
- China: Micius satellite (2017+) demonstrating intercontinental QKD, Beijing-Shanghai quantum network (2000+ km backbone)
- Europe: OPENQKD project building pan-European quantum network infrastructure
- United States: National Quantum Initiative funding quantum network research
- Financial sector: Limited pilot deployments for secure data center connections
Assessment: QKD provides information-theoretic security for specific high-value point-to-point links where cost and infrastructure requirements are justified. It will not replace internet-scale public-key cryptography due to scalability limitations and authentication dependencies.
Migration Strategy and Timeline
Why Gradual Transition is Necessary
Immediate full replacement of cryptographic infrastructure is infeasible:
- Backward compatibility: Billions of deployed devices lack PQC support
- Ecosystem maturity: Real-world deployment reveals implementation issues
- Cryptanalytic review: New algorithms require extended validation
- Operational risk: Hybrid approach provides fault tolerance
Hybrid Deployment Strategy
Security Model:
Hybrid constructions provide security if either classical or post-quantum component remains secure:
Security(Hybrid) = Security(Classical) ∨ Security(PQC)
This defends against:
- Classical attacks (protected by PQC component)
- Quantum attacks (protected by PQC component)
- Unknown PQC vulnerabilities (protected by classical component)
Industry Migration Timeline
2024-2025: Foundation (Current Phase)
- NIST published ML-KEM (FIPS 203), ML-DSA (FIPS 204), SLH-DSA (FIPS 205) in August 2024
- Cryptographic library integration: OpenSSL 3.0+, BoringSSL, wolfSSL, libOQS
- Vendor lab implementations and interoperability testing
- IETF drafting hybrid TLS 1.3 specifications
2025-2027: Pilot Deployments
- Early adopter organizations: defense contractors, financial services, healthcare
- Certificate Authorities begin issuing hybrid certificates (classical + PQC signatures)
- Cloud providers offer hybrid TLS endpoints for testing
- Internal enterprise deployments on non-critical systems
2027-2030: Accelerated Transition
- NIST mandate: Deprecate vulnerable algorithms by 2030
- Hybrid key exchange becomes standard for new TLS implementations
- Certificate chains transition to PQC signatures
- Active replacement of RSA-only PKI infrastructure
- Government agencies enforce PQC requirements for contractors
2030-2035: Post-Quantum Standard
- NIST mandate: Disallow vulnerable algorithms by 2035
- Pure PQC deployments become dominant
- Classical algorithms maintained only for backward compatibility with legacy systems
- Full replacement of RSA/ECC in TLS, S/MIME, SSH, VPN
- Estimated timeframe for cryptographically relevant quantum computers (CRQCs)
2035+: Complete Migration
- PQC mandatory for all new cryptographic systems
- Classical public-key cryptography relegated to compatibility layers
- Organizations complete re-encryption of long-term sensitive data
- Security certifications require PQC implementation
Implementation Roadmap for Organizations
Phase 1: Discovery and Assessment (0-6 Months)
1. Cryptographic Asset Inventory
Conduct comprehensive audit identifying all cryptographic implementations:
Key Exchange and Encryption:
- TLS endpoints: web servers, load balancers, API gateways, reverse proxies
- VPN infrastructure: IPsec gateways, SSL VPN concentrators
- Email security: S/MIME certificates, PGP keys
- Database encryption: TDE keys, column-level encryption
- Storage encryption: disk encryption, backup encryption
Digital Signatures:
- Code signing certificates: software distribution, firmware updates
- Document signing: PDF signatures, XML signatures
- PKI infrastructure: root CAs, intermediate CAs, OCSP responders
- SSH keys: system administration, automated processes
- IoT device provisioning: embedded certificates
Hardware:
- Hardware Security Modules (HSMs): inventory firmware versions
- Cryptographic accelerators: check PQC support roadmap
- Smart cards and tokens: assess replacement timeline
2. Data Sensitivity Classification
For each cryptographic system, assess confidentiality requirements:
Risk Assessment Framework:
Risk = Sensitivity × Exposure_Duration × Threat_Likelihood
Classification Tiers:
Tier 1 (Critical - Immediate Action Required):
- Data requiring 10+ years confidentiality
- Government classified material
- Healthcare PHI with long-term sensitivity
- Trade secrets and proprietary research
- Long-term financial records
Tier 2 (High - 1-2 Year Migration):
- Corporate communications and strategy
- Customer PII with moderate retention requirements
- Intellectual property with patent protection periods
Tier 3 (Medium - 3-5 Year Migration):
- Session data with limited lifetime
- Non-sensitive operational communications
- Public-facing services without confidential data
Phase 2: Architecture and Testing (6-12 Months)
1. Crypto-Agility Implementation
Design systems for algorithm flexibility:
Architecture Principles:
# Anti-pattern: Hard-coded algorithm
def encrypt_data(data):
cipher = AES.new(key, AES.MODE_GCM)
return cipher.encrypt(data)
# Correct: Configurable algorithm
def encrypt_data(data, algorithm='AES-256-GCM'):
cipher_class = get_cipher(algorithm)
cipher = cipher_class.new(key, get_mode(algorithm))
return cipher.encrypt(data)
Configuration Management:
- Externalize algorithm selection to configuration files
- Implement protocol version negotiation
- Support multiple algorithms simultaneously during migration
- Design for rollback capability if issues discovered
2. Laboratory Validation
Test Environment Setup:
- Deploy hybrid TLS 1.3 on isolated internal network
- Configure test CA to issue ML-DSA certificates
- Implement ML-KEM key encapsulation in test applications
- Measure performance metrics: latency, throughput, resource utilization
Performance Benchmarking:
Metrics to collect:
- TLS handshake latency (classical vs hybrid)
- Certificate chain validation time
- CPU utilization during key operations
- Memory footprint increase
- Network bandwidth consumption
- Session establishment rate
Compatibility Testing:
- Client/server interoperability across vendors
- Legacy client behavior with hybrid endpoints
- Protocol fallback mechanisms
- Error handling and logging
3. Infrastructure Capacity Assessment
Network:
- Certificate size increase: ~1-2 KB per certificate in chain
- Handshake message size: hybrid adds ~1-2 KB to ClientHello/ServerHello
- Bandwidth impact analysis for high-volume environments
Compute:
- ML-KEM operations: ~2-5 ms per handshake on modern CPUs
- ML-DSA signature generation: ~5-10 ms
- ML-DSA signature verification: ~2-5 ms
- Aggregate impact on load balancer capacity
Storage:
- Certificate store capacity (larger certificates)
- Key material database expansion
- Backup and replication bandwidth
Monitoring:
- Update SIEM parsers for hybrid TLS handshake messages
- Instrument PQC algorithm usage metrics
- Alert on PQC-specific error conditions
Phase 3: Controlled Deployment (1-3 Years)
1. Phased Migration by Risk Tier
Year 1: Tier 1 Systems
- Internal VPN infrastructure (lower risk, high value)
- Internal web applications (controlled user base)
- Development and staging environments (safe testing ground)
- Internal certificate authorities (prepares for broader deployment)
Year 2: Tier 2 Systems
- Customer-facing APIs (with fallback to classical)
- Email infrastructure (S/MIME hybrid certificates)
- Code signing pipeline (software distribution)
- Administrative SSH keys (system access)
Year 3: Tier 3 Systems
- Public-facing web properties
- Legacy systems with extended replacement timelines
- Partner integration endpoints (requires coordination)
2. Hybrid Certificate Deployment
Certificate Chain Structure:
Root CA (RSA-4096 + ML-DSA-87)
└─ Intermediate CA (ECDSA-P384 + ML-DSA-65)
└─ End Entity (ECDSA-P256 + ML-DSA-44)
Migration Strategy:
- Issue new intermediate CAs with hybrid signatures
- Distribute hybrid root certificates to clients via software updates
- Maintain classical-only certificates for backward compatibility during transition
- Implement OCSP with hybrid signatures
3. VPN and Email Migration
IPsec VPN:
- Deploy hybrid IKEv2 with ECDH + ML-KEM key exchange
- Update VPN clients to support hybrid algorithms
- Maintain classical-only support for legacy endpoints
- Monitor connection success rates and failure modes
S/MIME Email:
- Issue hybrid certificates to users
- Configure mail servers to prefer hybrid algorithms
- Maintain classical signature support for external recipients
- Implement transparent fallback for non-PQC clients
Phase 4: Full Transition (3-10 Years)
1. Production Deployment
- Transition public-facing TLS to hybrid by 2028-2029 (ahead of NIST 2030 deprecation)
- Complete certificate re-issuance across enterprise
- Re-encrypt long-term archived data with PQC-protected keys
- Decommission classical-only cryptographic systems
2. Legacy System Handling
Systems Unable to Migrate:
- Increase classical key sizes: RSA-4096 minimum, ECDSA P-384
- Implement aggressive key rotation: quarterly or monthly
- Isolate from sensitive data flows where possible
- Document compensating controls and residual risk
- Establish sunset dates for final decommissioning
3. Continuous Monitoring
Quantum Computing Progress:
- Track qubit count and error rates from major vendors (IBM, Google, IonQ, Rigetti)
- Monitor academic publications for algorithmic improvements (Shor optimization, error correction advances)
- Assess NIST cryptanalytic reviews and algorithm updates
Cryptanalytic Developments:
- Subscribe to IACR ePrint for lattice cryptanalysis papers
- Monitor NIST PQC forum for vulnerability disclosures
- Participate in industry information sharing groups
- Maintain readiness to rotate algorithms if weaknesses discovered
Compliance and Standards:
- Track NIST Special Publications for updated guidance
- Monitor industry-specific regulations (HIPAA, PCI-DSS, FedRAMP)
- Align with CISA and NSA recommendations
- Prepare for post-quantum cryptography audits
Example: Enterprise Migration Case Study
Organization Profile: TechCorp Inc.
Infrastructure:
- E-commerce platform (100K daily TLS sessions)
- Corporate VPN (5,000 remote employees)
- Email infrastructure (10,000 users with S/MIME)
- CI/CD pipeline (code signing for software releases)
- Internal PKI (1 root CA, 3 intermediate CAs, 500+ end-entity certificates)
Migration Execution:
Phase 1 (2024-2025): Discovery
- Conducted cryptographic inventory: identified 387 TLS certificates, 3 VPN gateways, 2 email servers, 1 code-signing certificate, 4 CAs
- Risk assessment: e-commerce and email classified Tier 2 (customer PII); VPN and internal systems Tier 3
- Budget allocation: $500K for HSM upgrades, consulting, and testing infrastructure
- Vendor engagement: confirmed load balancer PQC support roadmap from F5
Phase 2 (2025-2026): Testing
- Deployed hybrid TLS in lab environment using OpenSSL 3.2
- Performance testing: measured 3ms latency increase per TLS handshake (acceptable)
- Discovered certificate size issue in legacy database (VARCHAR(4096) column insufficient); remediated
- Procured updated HSM firmware supporting ML-KEM and ML-DSA operations
- Completed compatibility matrix for client browser versions
Phase 3 (2026-2027): Internal Deployment
- Q1 2026: Deployed hybrid TLS on corporate VPN (5,000 users migrated successfully)
- Q2 2026: Migrated internal web applications to hybrid (monitored for 90 days, no issues)
- Q3 2026: Issued hybrid S/MIME certificates to 10,000 employees via internal CA
- Q4 2026: Updated code-signing pipeline with ML-DSA signatures
- Metrics: 99.8% success rate, 0.2% clients required fallback to classical
Phase 4 (2027-2028): External Deployment
- Q1 2027: Enabled hybrid TLS on e-commerce platform behind feature flag (10% traffic)
- Q2 2027: Increased hybrid traffic to 50%, monitored conversion rates and error logs
- Q3 2027: Full production rollout of hybrid TLS (100% traffic)
- Q4 2027: Replaced all public-facing certificates with hybrid signatures
- Results: No measurable impact on conversion rates; 0.1% error rate from ancient clients (Android 4.x)
Ongoing (2028+):
- Quarterly reviews of quantum computing developments
- Annual cryptographic posture assessments
- Maintained classical fallback support until 2032
- Completed full migration to pure PQC by 2033
Total Cost: $2.1M over 8 years (HSMs, consulting, labor, testing infrastructure)
Risk Reduction: Eliminated quantum decryption risk for all forward secrecy sessions
Key Takeaways
Current Cryptographic Landscape
Symmetric Cryptography (AES-256):
Remains secure with proper implementation. Operates through substitution-permutation network (SubBytes, ShiftRows, MixColumns, AddRoundKey) over 14 rounds for 256-bit keys. Primary attack vector is brute force, which remains computationally infeasible with appropriate key lengths.
Asymmetric Cryptography - RSA:
Security derives from integer factorization hardness. Typically deployed with 2048-4096 bit moduli. Common applications include legacy key transport and digital signatures. Vulnerable to Shor's algorithm.
Asymmetric Cryptography - ECC:
Security based on elliptic curve discrete logarithm problem (ECDLP). Uses 256-384 bit keys providing equivalent security to larger RSA keys. Standard for modern TLS 1.3 implementations. Vulnerable to Shor's algorithm.
Digital Signatures:
Provide authentication and integrity guarantees. Certificate chains establish transitive trust from end-entity certificates to trusted root Certificate Authorities.
TLS 1.3 Protocol:
Employs ECDHE for forward-secret key agreement and authentication, transitions to AES-GCM or ChaCha20-Poly1305 for bulk data confidentiality and integrity.
Quantum Threat Assessment
Shor's Algorithm:
Executes integer factorization and discrete logarithm computation in polynomial time O((log N)³) on quantum computers. Reduces RSA and ECC security from exponential to polynomial complexity—transforming cryptanalysis from infeasible (10^20+ operations) to practical (achievable in hours to weeks with ~1M qubits).
Grover's Algorithm:
Provides quadratic speedup for unstructured search: O(√N) versus classical O(N). Reduces effective security of symmetric algorithms by half (AES-256 → 128-bit effective security). Mitigation: use AES-256 instead of AES-128.
Harvest Now, Decrypt Later (HNDL):
Active threat model where adversaries collect encrypted traffic today for retroactive decryption once CRQCs emerge. Critical risk for data requiring confidentiality beyond 2030-2035. Affects government communications, healthcare records, intellectual property, and long-term business strategies.
Post-Quantum Solutions
ML-KEM (FIPS 203):
Lattice-based key encapsulation mechanism. Replaces ECDH in TLS handshakes and VPN key exchange. Security foundation: Module Learning With Errors (Module-LWE). Parameter sets provide 128/192/256-bit quantum security levels. Public keys: 800-1,568 bytes; ciphertexts: 768-1,088 bytes.
ML-DSA (FIPS 204):
Lattice-based digital signature algorithm. Replaces ECDSA/RSA for certificate signing, code signing, and document authentication. Security foundation: Module-LWE with Fiat-Shamir transformation. Signature sizes: 2,420-4,627 bytes depending on security level.
SLH-DSA (FIPS 205):
Stateless hash-based signature scheme. Conservative alternative for long-term archives and high-assurance applications. Security foundation: cryptographic hash function security only (no novel assumptions). Signature sizes: 7,856-49,856 bytes. Ideal for scenarios requiring maximum confidence over decades.
Hybrid Cryptography:
Combines classical and post-quantum algorithms to hedge against implementation vulnerabilities and cryptanalytic breakthroughs. Provides security if either component remains secure: Security(Hybrid) = Security(Classical) ∨ Security(PQC).
Implementation Impact
End User Experience:
- TLS handshake latency increase: 2-5 milliseconds (imperceptible)
- Certificate size increase: 1-2 KB per certificate chain
- Browser compatibility: transparent with modern browsers
- Overall impact: minimal to negligible
Infrastructure Requirements:
- Certificate storage capacity adjustment for larger certificates
- Network bandwidth minor increase for handshake messages
- Computational overhead: typically <5% for most workloads
- Monitoring updates to parse hybrid protocol messages
Developer Considerations:
- Adopt cryptographic libraries with PQC support (OpenSSL 3.0+, BoringSSL, wolfSSL)
- Implement crypto-agility patterns (configurable algorithms, protocol versioning)
- Test hybrid implementations in staging environments
- Document algorithm selections and security rationale
- Plan migration timelines aligned with organizational risk tolerance
Strategic Imperatives
Timeline Compression:
Recent algorithmic optimizations reduced RSA-2048 breaking requirements from 20 million to <1 million qubits. Combined with rapid quantum hardware progress (1,000+ qubit systems now operational), the threat timeline has compressed from 20+ years to potentially 5-10 years. Organizations cannot afford "wait and see" strategies.
Regulatory Compliance:
NIST mandates deprecation of quantum-vulnerable algorithms by 2030, complete disallowance by 2035. Federal agencies and contractors must comply. Industry sectors (healthcare, finance) will follow with regulatory requirements.
Risk Management:
Organizations protecting data requiring 10+ year confidentiality must deploy PQC now. Waiting until CRQCs emerge forces choice between rushed migration (error-prone, expensive) or accepting breach risk (unacceptable for sensitive data).
Conclusion: The Quantum Transition is Underway
Quantum computers will break RSA and ECC—this is mathematical certainty, not speculation. The uncertainty lies in precise timeline, but current trends indicate RSA-2048 could be compromised by 2030.
The window for proactive migration is narrowing:
2025-2027: Organizations should complete cryptographic inventories, test hybrid implementations, and begin internal deployments.
2027-2030: Production migration of customer-facing systems must accelerate to meet NIST deprecation deadline.
2030-2035: Complete transition to PQC-dominant infrastructure before NIST disallowance and potential CRQC emergence.
Organizations that execute systematic migrations now will achieve seamless transitions with minimal operational disruption. Organizations that delay face emergency responses under adverse conditions—compressed timelines, limited vendor support, potential data breaches, and compliance violations.
Your cryptographic posture in 2030 is determined by actions taken in 2025. The quantum threat is not hypothetical future risk—it is present operational reality demanding immediate strategic response.
Recommended Immediate Actions:
- Initiate cryptographic inventory this quarter — You cannot protect assets you haven't identified
- Assess data sensitivity and retention requirements — Prioritize systems protecting long-term confidential data
- Establish PQC working group — Cross-functional team (security, infrastructure, development, compliance)
- Deploy laboratory test environment — Validate hybrid TLS and PQC certificate operations
- Engage vendors on PQC roadmaps — Ensure infrastructure components support transition
- Develop migration timeline — Align with NIST deadlines and organizational risk tolerance
- Allocate budget for 2025-2030 transition — HSM upgrades, consulting, testing infrastructure, labor
The post-quantum cryptographic transition represents the most significant cryptographic migration since the shift from DES to AES. Organizations that treat this as strategic priority will maintain security and competitive advantage. Organizations that underestimate urgency will face crises.