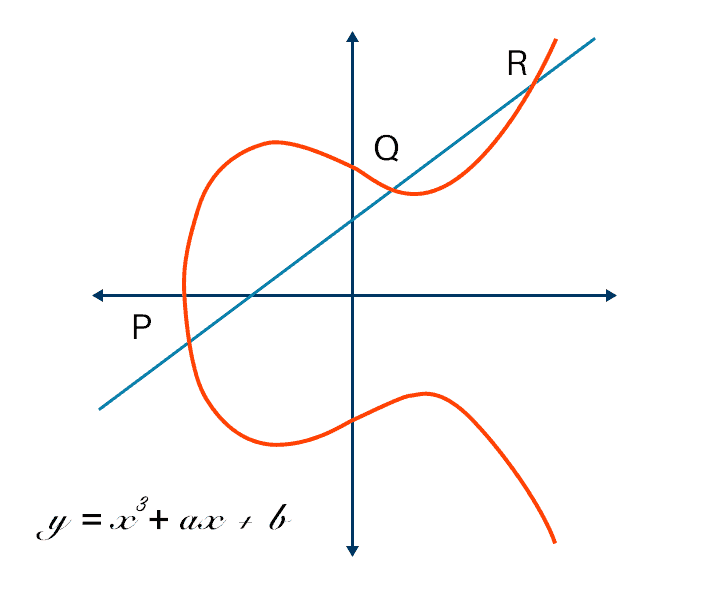Modern Cryptography, Part I
This article portrays the importance of Cryptographic Algorithms and how the modern age digital eco-systems are being protected. Understanding what algorithms are being used now and what's about to happen in near future.
Introduction
The security of the internet basically depends on two main kinds of encryption. Symmetric and asymmetric cryptography form the core of it all. This mix has protected our online lives for many years now.
You log into your bank, send off a personal message, or watch something on Netflix. Encryption runs quietly behind the scenes each time. RSA takes care of your login details. ECC handles security in your chat apps. AES makes sure no one snoops on your web links.
These methods stand as the main support for cybersecurity today. They prove mathematically clean and quick to use. Current computers just cannot crack them in any real way.
This blog looks at the true inner workings of these setups. It skips heavy math equations. It avoids tough technical terms too. The focus stays on the straightforward processes that guard the web we use every day.
Part 1: The Three Pillars of Modern Cryptography
Before diving into how encryption works, you need to understand what we're actually trying to protect:
The Three Security Goals
CIA Triad
- Confidentiality – Nobody except the intended recipient can read the message.
- Authenticity – The receiver knows the message came from the claimed sender
- Integrity – The receiver knows the message wasn't altered in transit.
Real-world protocols like HTTPS, VPNs, and Signal combine three different cryptographic tools to achieve all three goals:
- Symmetric encryption (like AES) – Fast, encrypts massive amounts of data.
- Asymmetric encryption (like RSA and ECC) – Solves the key exchange problem, enables authentication.
- Cryptographic hashing (like SHA-256) – Detects tampering, derives keys.
The beauty of modern security is that each tool does one job exceptionally well.
Part 2: Symmetric Encryption
The Concept
Symmetric encryption is simple: both parties share the exact same secret key, and they use it to lock and unlock messages.
Think of a physical safe:
- Alice and Bob both have the same combination: 4729.
- Alice puts a document in the safe, locks it, and sends it to Bob.
- Bob opens it with the same combination.
- An attacker with the safe but no combination can't open it.
In digital form, this is AES (Advanced Encryption Standard) — the encryption used in:
- HTTPS (every secure website)
- VPNs (like NordVPN, Mullvad)
- Full-disk encryption (BitLocker, FileVault)
- Messaging apps (WhatsApp, Signal use AES internally)
- WiFi encryption (WPA3 uses AES)
Why AES is Used Everywhere
It's fast. A modern CPU can encrypt 1GB of data in seconds using AES. This matters for streaming video, real-time calls, and high-throughput servers.
It's proven. AES was selected in a public competition by the U.S. government in 2001 and has survived 20+ years of cryptanalysis without breaking.
It's simple to implement correctly (relatively speaking).
How AES Works: The Four-Step Scrambling
AES encrypts data in 128-bit chunks (16 bytes) and puts each chunk through a series of scrambling operations.
Imagine you want to encrypt:
"HELLOWORLD!!!!!" (16 characters = 16 bytes = 1 block)
Round Structure:
AES performs 10, 12, or 14 identical rounds (depending on key size) with four operations each:
1. SubBytes – Character Substitution
Every byte gets replaced using a lookup table (called an S-box).
Think of it like a substitution cipher:
- Original byte value: 65 (ASCII for 'A')
- S-box lookup: 65 → 152
- The byte is now 152
This happens to all 16 bytes simultaneously.
Why it matters: This non-linear substitution is what makes brute-forcing impossible. Without it, the cipher would be reversible through math alone.
2. ShiftRows – Positional Rearrangement
The 16 bytes shuffle their positions:
Before: [A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P]
After: [A, F, K, P, B, G, L, E, C, H, M, I, D, J, N, O]
(simplified example)
Why it matters: This mixes bytes from different parts of the plaintext, ensuring a change in one position affects multiple output positions.
3. MixColumns – Byte Interaction
Each column of 4 bytes is mathematically blended so every output byte depends on all 4 input bytes in that column.
Why it matters: This creates diffusion—a single changed bit in the plaintext affects multiple bytes in the ciphertext, making pattern recognition impossible.
4. AddRoundKey – Key Mixing
The 16 bytes are combined with a round key (derived from the main encryption key) using XOR (bit-by-bit comparison).
Each of the 10-14 rounds uses a different round key.
Why it matters: Without this, the cipher would be deterministic and symmetry-breakable.
The Avalanche Effect
Here's what makes AES unbreakable: change one letter, and the entire output changes unpredictably.
Encrypt "HELLOWORLD!!!!!" → get ciphertext A
Encrypt "HELLOWORLD!!!!" X" (one character changed) → get completely different ciphertext B
An attacker can't compare similar messages to deduce patterns or the key.
Why AES is Secure (The Brute Force Reality)
The only practical attack against AES is brute force: try every possible key until one works.
AES-256 (the standard for high security) has 2256 possible keys.
That's approximately
78,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 keys.
Even if an attacker could test 1 billion billion keys per second (orders of magnitude faster than today's fastest computers), it would take longer than the age of the universe to try them all.
Bottom line: AES is secure as long as the key is random and kept secret.
AES in Real TLS Connections
When you visit 'https://google.com', the actual data encryption looks like:
1. Browser and server agree on AES-256-GCM (via key exchange, see below)
2. Browser generates a random 256-bit key
3. Both sides use this key to encrypt/decrypt all traffic until connection closes
4. Each message is encrypted independently with AES
5. GCM mode also authenticates, detecting tampering
Part 3: The Key Exchange Problem – Why Asymmetric Crypto Exists
Here's the problem that has vexed cryptographers for centuries:
Two people need to agree on a secret key, but they're communicating over an open, monitored network.
If Alice sends the symmetric key to Bob in plain text, an attacker listening on the network just captures it. Game over.
This is why asymmetric cryptography (public-key cryptography) was invented.
The Brilliant Idea: Two Different Keys
Instead of one shared key, asymmetric crypto uses a key pair:
- Public Key – Can be shared with anyone, posted online, published in directories
- Private Key – Never leaves your device, never shared, never revealed
Mathematical magic ensures:
- Anything encrypted with the public key can only be decrypted with the private key
- Anything signed with the private key can only be verified with the public key
This solves the key distribution problem entirely.
Part 4: RSA (Rivest-Shamir-Adleman) Encryption Algorithm
The "Big Number Factoring" Lock
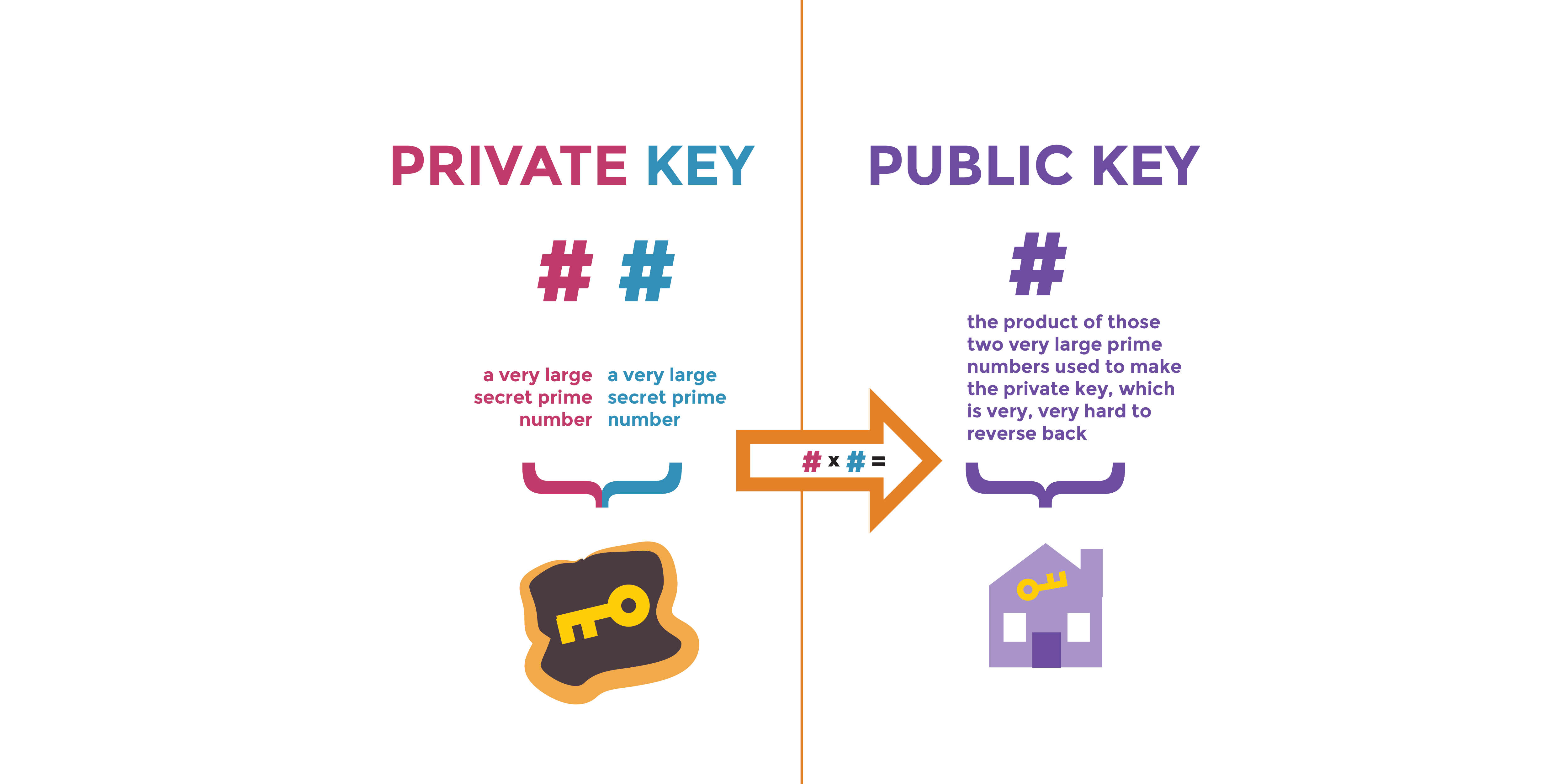
The Core Insight
RSA's security rests on a single mathematical fact: Multiplying two large prime numbers together is trivially easy. Factoring the result back into the original primes is computationally impossible.
RSA Key Generation: Step by Step
Step 1: Pick Two Large Prime Numbers
In real systems, each prime is roughly 1,024+ digits long (cryptographers call this "1024-bit").
For illustration, let's use tiny primes:
p = 61
q = 53
Step 2: Multiply Them
n = p × q = 61 × 53 = 3,233
This number n = 3,233 is your public key component. It's used to encrypt messages for you.
In real RSA, n is a 600+ digit number. Factoring that back into the original primes would take billions of years on a classical computer.
Step 3: Calculate a "Magic Number" Based on the Primes
There's a mathematical calculation (Euler's totient) that depends on p and q:
For our example: φ(n) = (p-1) × (q-1) = 60 × 52 = 3,120
This number is used internally but never shared.
Step 4: Choose Your Public Exponent `e`
This is almost always 65,537 (chosen for efficiency). It must be chosen so that it doesn't share common factors with φ(n).
For our example: e = 17
Your public key is now: (n=3,233, e=17)
Anyone can have this. It's safe to post on your website.
Step 5: Calculate Your Private Exponent `d`
Using mathematical calculations, find a number `d` such that when you use it with `e`, they "undo" each other in a special way.
For our example: d = 2,753
Your private key is now: (n=3,233, d=2,753)
Critical: Destroy p, q and φ(n) completely. They're only used for key generation.
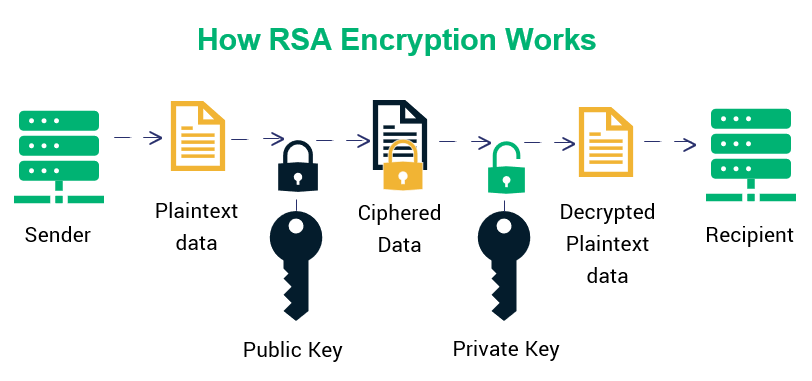
RSA Encryption: Sending a Secret Message
Alice wants to send the letter "A" to Bob.
Step 1: Bob Shares His Public Key
Bob publishes: (n=3,233, e=17)
Step 2: Alice Converts Her Message to a Number
The letter "A" in ASCII is 65.
Step 3: Alice "Raises" the Message to the Power of `e`, Then Takes the Result Modulo `n`.
Conceptually (simplified): ciphertext = messagee mod n
In our example:
6517 mod 3,233 = 2,790
Step 4: Alice Sends the Ciphertext
Alice sends: 2,790
An eavesdropper sees:
- Ciphertext: 2,790
- Public key: (n=3,233, e=17)
- But cannot decrypt without `d`
RSA Decryption: Only Bob Can Read It
Step 1: Bob Receives the Ciphertext
Bob receives: 2,790
Step 2: Bob Uses His Private Exponent `d`
Bob computes: plaintext = 2,7902,753 mod 3,233 = 65 = "A"
Bob recovers the original message.
Why Can Only Bob Decrypt it:
To decrypt, an attacker would need to find `d`.
To find `d`, they'd need φ(n) = 3,120.
To find φ(n), they'd need to factor n = 3,233 back into p = 61 and q = 53.
With our tiny numbers, factoring is easy:
- Try dividing 3,233 by small primes
- Eventually find that 3,233 = 61 × 53
But with real RSA-2048 (600-digit `n`), there are no efficient classical algorithms to factor it. The best known methods would take billions of years.
Real World Applications of RSA:
1. HTTPS Certificates
Your browser trusts HTTPS because of RSA signatures on certificates:
1. Certificate Authority (CA) has an RSA key pair
2. When you request an HTTPS certificate for example.com,
the CA verifies you own the domain
3. The CA signs your certificate with their private key
4. Your certificate is sent to browsers
5. Browsers verify the signature using the CA's public key
(shipped with the browser)
6. If the signature is valid, the browser trusts your identity
This chain of trust is how HTTPS knows you're actually communicating with Amazon, not an attacker.
2. TLS Key Exchange (Older Protocol)
Older TLS versions used RSA for key exchange (TLS 1.2 and earlier allowed it):
1. Client has server's public key from certificate
2. Client generates a 256-bit symmetric key
3. Client encrypts it with server's RSA public key
4. Server decrypts it with its RSA private key
5. Both have the symmetric key; now use AES for data
Modern TLS 1.3 abandoned this because it's slower than elliptic curve key exchange (coming next).
3. Code and Document Signing
Developers sign code with RSA to prove they wrote it:
1. Developer hashes their code (produces a unique fingerprint)
2. Developer encrypts the hash with their RSA private key (creates signature)
3. User downloads code + signature
4. User verifies signature using developer's public key
5. If valid, code is authentic and unaltered
RSA: Practical Numbers
- Typical key size: 2,048 bits (256 bytes) for current security
- Future recommendation: 4,096 bits (512 bytes) for long-term security
- Signature size: 256 bytes
- Encryption overhead: Requires padding, so actual data is smaller
- Speed: Slower than symmetric crypto (used only for key exchange and signatures)
Part 5: Elliptic Curve Cryptography (ECC) – The "Compact, Efficient" Alternative
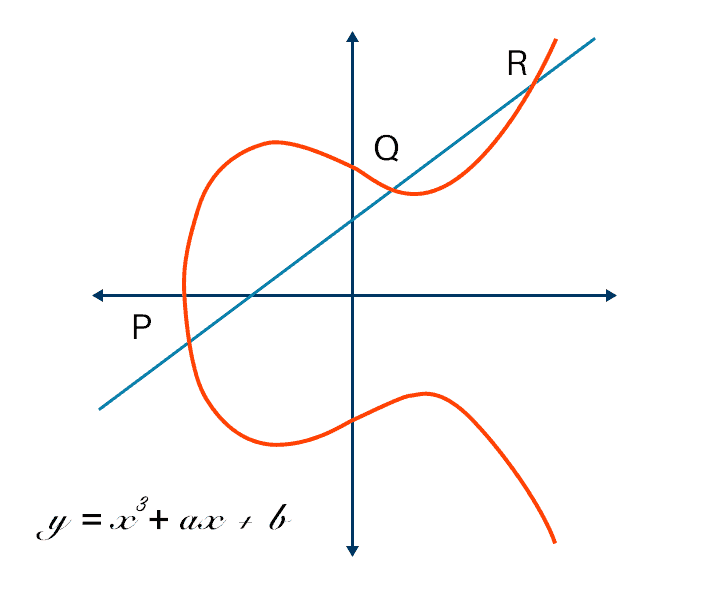
Why ECC Exists
RSA works perfectly but has one problem: large key sizes.
To achieve 256-bit security (equivalent to AES-256):
- RSA: Need ~15,000-bit keys (1,875 bytes)
- ECC: Need ~256-bit keys (32 bytes)
ECC is 60× smaller for identical security.
This matters for:
- Mobile devices with limited storage
- IoT devices with minimal processing power
- Bandwidth constraints
- Speed (smaller keys = faster operations)
Modern systems strongly prefer ECC: TLS 1.3, Signal, WhatsApp, Bitcoin, Ethereum, and modern APIs all use ECC.
The Elliptic Curve: A Geometric Concept
An elliptic curve is a curve defined by the equation:
y = x³ + ax + b
Where:
- a and b are constants chosen for the specific curve
- All arithmetic happens in a finite field (modulo a large prime)
- The curve contains thousands of billions of points
The special property: You can define an "addition" operation on points of this curve that creates a group structure.
How "Addition" Works on Elliptic Curves
This isn't normal addition. Here's the geometric idea:
1. To add point P to point Q:
- Draw a line through P and Q
- The line intersects the curve at a third point R
- Reflect R across the x-axis
- That reflection is your result: P + Q
2. To add a point to itself (P + P):
- Draw a tangent line to the curve at P
- The tangent intersects the curve at another point R
- Reflect R across the x-axis
- That's your result: 2P
3. To add P multiple times:
- P + P + P = 3P (add P to itself 3 times)
- Conceptually: kP = P + P + ... + P (k times)
The key insight: You can easily compute `kP` (P added to itself k times), but if someone gives you `kP` and `P`, finding k is computationally infeasible.
This is the Elliptic Curve Discrete Logarithm Problem (ECDLP), and it's the foundation of ECC security.
ECDH: Elliptic Curve Diffie-Hellman Key Agreement
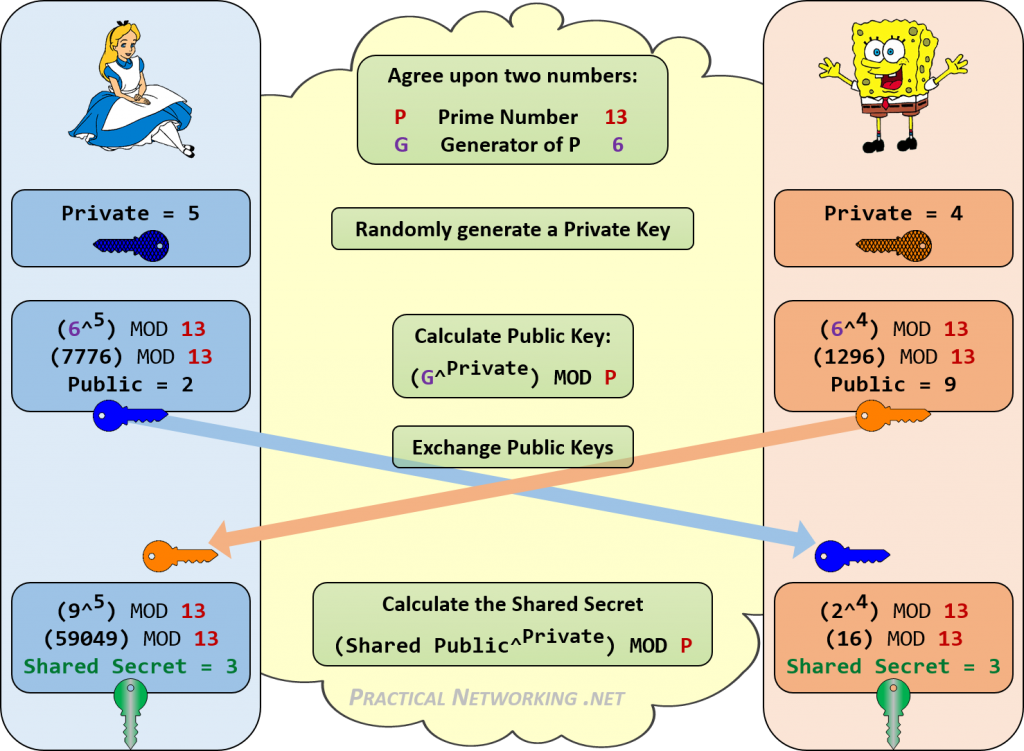
ECDH solves the key exchange problem using elliptic curves.
Setup (Public Knowledge)
Alice and Bob agree on:
- A specific elliptic curve (like Curve25519 or P-256)
- A starting point 'G' on that curve
The Protocol
Alice's Side:
1. Pick a random private number: a = 42 (only Alice knows this)
2. Compute her public key by adding P to itself 42 times: A = 42G
3. Send A to Bob over the open network
Bob's Side:
1. Pick a random private number: b = 17 (only Bob knows this)
2. Compute his public key by adding G to itself 17 times: B = 17G
3. Send B to Alice over the open network
Alice's Computation of Shared Secret:
1. Receive Bob's public key: B = 17G
2. Multiply it by her private key: S = 42 × B = 42 × (17G)
3. Result: S = (42 × 17) × G = 714G
Bob's Computation of Shared Secret:
1. Receive Alice's public key: A = 42G
2. Multiply it by his private key: S = 17 × A = 17 × (42G)
3. Result: S = (42 × 17) × G = 714G
The Magic: Both Alice and Bob computed the same point '714G'!
Why an Eavesdropper Can't Compute It
An attacker sees:
- Alice's public key: 42G
- Bob's public key: 17G
- But doesn't have 42 or 17
To compute the shared secret 714G, they'd need to either:
- Find 42 from 42G (solving ECDLP), or
- Find 17 from 17G (solving ECDLP)
Both are computationally infeasible.
ECDSA: Elliptic Curve Digital Signature Algorithm
ECDSA is the ECC equivalent of RSA signatures. It's used to sign:
- HTTPS certificates
- Software updates
- Bitcoin transactions
- Legal documents
Signing a Document
Bob wants to sign a message to prove he created it.
Step 1: Bob hashes the message (produces a unique fingerprint)
Example:
hash("I authorize this payment") = 789
Step 2: Bob generates a random nonce k
Example:
k = 55 (used only once, then discarded)
Step 3: Bob computes a point on the curve using k
- Point = 55G (add G to itself 55 times)
- Extract x-coordinate of this point, call it r
- r = (x-coordinate of 55G) mod curve_order
Step 4: Bob creates the signature combining his private key, the hash, and `r`
s = k^-1 × (hash + r × private_key) mod curve_order
s = 55^-1 × (789 + r × bob's_private_key) mod curve_order
(^-1 means "modular inverse" - a specific mathematical operation)
Step 5: Signature is the pair (r, s)
Verifying the Signature
Alice receives Bob's message and signature (r, s).
Step 1: Alice hashes the message herself
hash("I authorize this payment") = 789 (same as Bob)
Step 2: Alice performs a calculation using:
- The signature values r and s
- The message hash
- Bob's public key
Point = (s^-1 × hash × G) + (s^-1 × r × bob_public_key)
Step 3: Extract the x-coordinate of this point
Step 4: If the x-coordinate equals r, the signature is valid!
Why Forgery is Impossible
To forge Bob's signature, you'd need to create a valid (r, s) pair without knowing Bob's private key.
This is mathematically equivalent to solving ECDLP (finding the private key from the public key).
With Curve25519 or P-256, this is computationally impossible.
Curve Selection: What's Actually Used
- P-256 is used in: iPhones, Android, TLS certificates, government systems, NIST standard; some debate about design transparency.
- Curve25519 is used in: Signal, WireGuard VPN, modern TLS | Designed for security and resistance to implementation errors.
- secp256k1 is used in: Bitcoin, Ethereum | Chosen for efficiency, not part of NIST standards.
- P-384, P-521 is used in: High-security applications | Larger curves for 192-bit and 256-bit security levels.
Part 6: Modern TLS – Symmetric, Asymmetric, and Hash Functions Working Together
To understand why quantum computers are a threat, you need to see how these three cryptographic tools work together in practice.
A Real HTTPS Connection: Step by Step
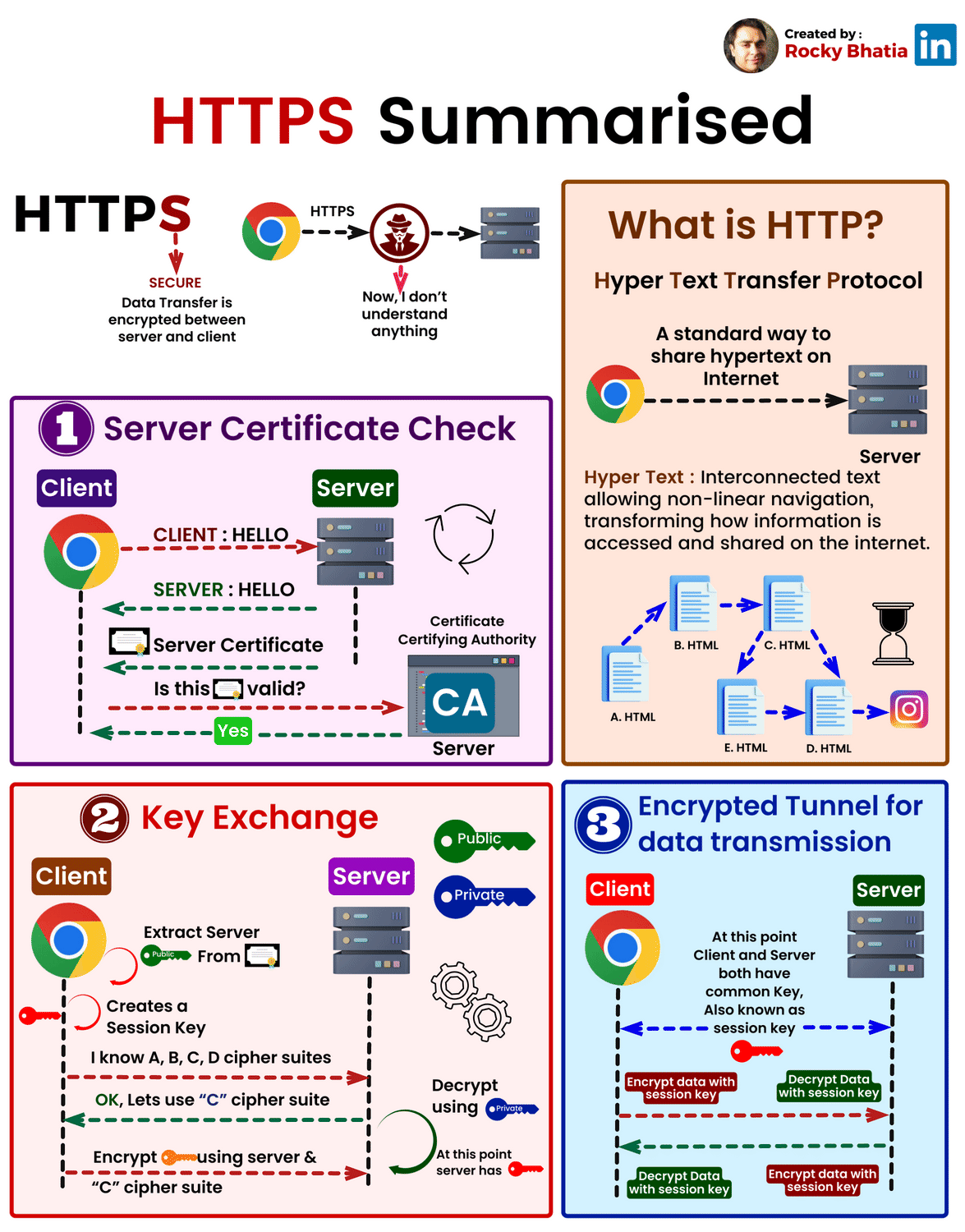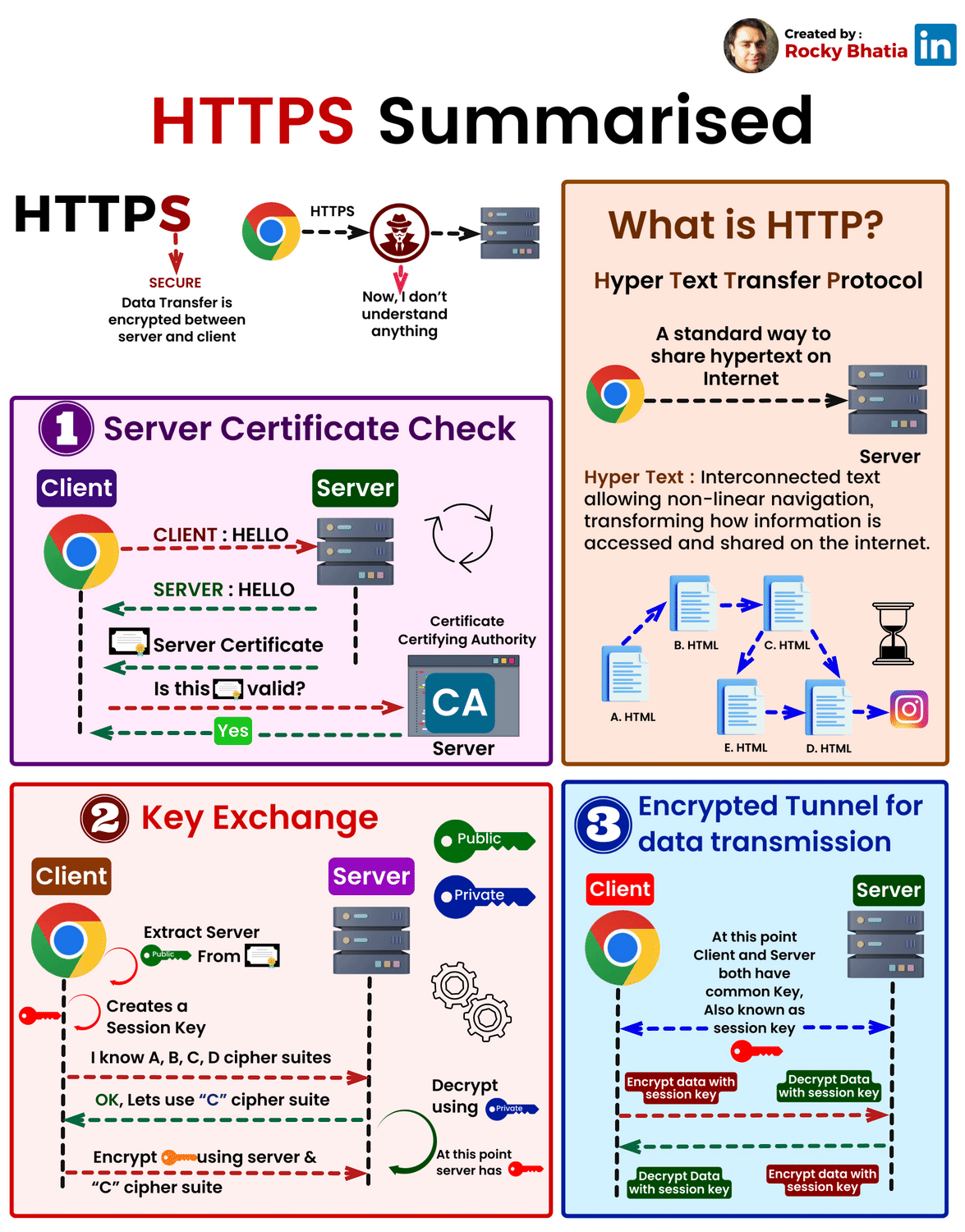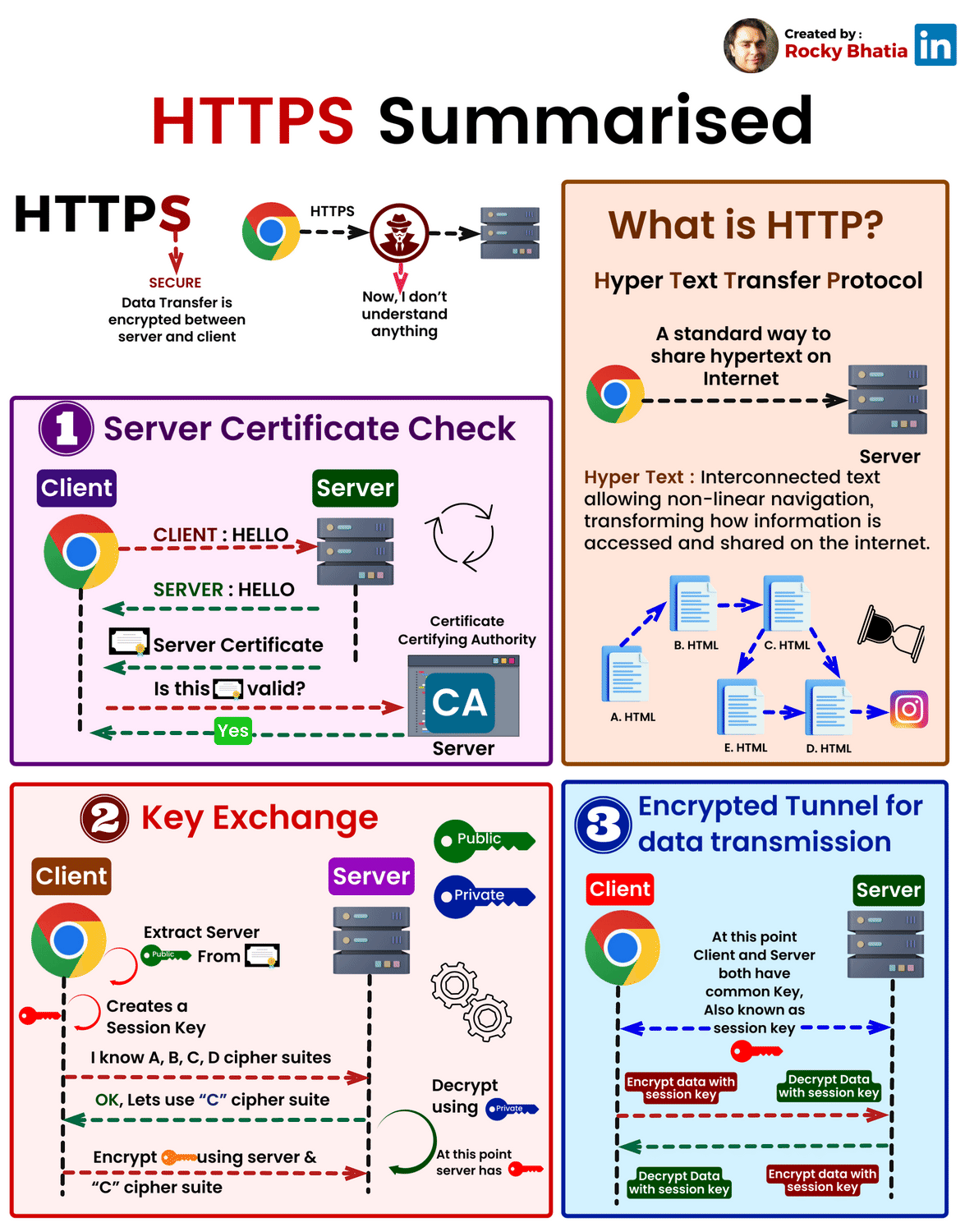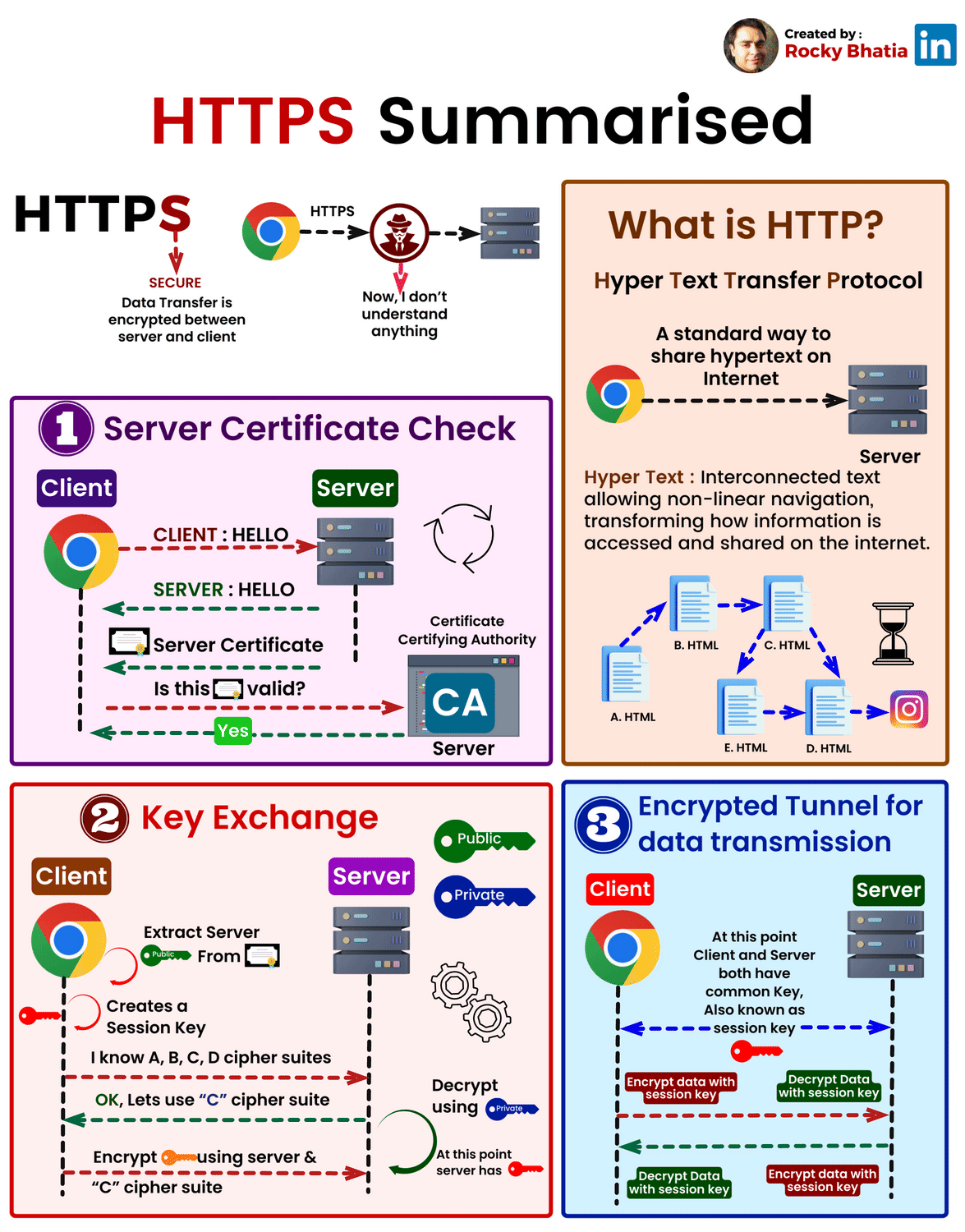
When you visit 'https://amazon.com', here's exactly what happens:
Step 1: ClientHello
Your browser initiates a connection:
"Hi Amazon, I'd like a secure connection.
I support these elliptic curves: P-256, Curve25519, etc.
I support these symmetric ciphers: AES-128-GCM, AES-256-GCM, ChaCha20-Poly1305"
The browser also sends its ephemeral public key (generated fresh for this connection).
Step 2: ServerHello
Amazon responds:
"Great! I've chosen:
- Elliptic Curve: Curve25519
- Symmetric Cipher: AES-256-GCM
Here's my certificate with my long-term public key
Here's my ephemeral public key for this session"
Amazon also includes a digital signature on the handshake messages (using ECDSA).
Step 3: Certificate Verification
Your browser receives Amazon's certificate and checks:
1. Is this certificate signed by a trusted CA?
- Your browser has the CA's public key
- Uses ECDSA verification to check the signature is valid
- If valid, the CA approved Amazon's identity
2. Does the domain name match?
- Certificate says: "This is for amazon.com"
- URL bar shows: "amazon.com"
- Match? ✓
3. Is it expired?
- Certificate says: "Valid until 2025-12-15"
- Today is: 2025-12-04
- Valid? ✓
If all checks pass, the browser trusts Amazon's identity.
Step 4: ECDH Key Agreement
Your browser now has:
- Amazon's ephemeral public key (from ServerHello)
- Your ephemeral private key (generated in Step 1)
Both you and Amazon compute the same ECDH shared secret:
Your computation: your_private_key × amazon_ephemeral_public_key = SHARED_SECRET
Amazon's computation: amazon_private_key × your_ephemeral_public_key = SHARED_SECRET
(These are identical due to elliptic curve math)
Critical: This ECDH secret is temporary—it's destroyed after the connection closes.
Step 5: Derive Symmetric Keys
The ECDH shared secret is fed into a **Key Derivation Function (KDF)** with other parameters:
symmetric_key = KDF(ecdh_shared_secret, client_random, server_random, "key")
mac_key = KDF(ecdh_shared_secret, client_random, server_random, "mac")
Both sides now have:
- A 256-bit AES encryption key
- A key for authentication (message authentication code)
These keys are generated fresh for each TLS connection and never reused.
Step 6: Encrypted Communication
Everything from now on is encrypted with AES-256-GCM:
Browser → Amazon: GET / HTTP/1.1 [ENCRYPTED WITH AES-256-GCM]
Amazon → Browser: 200 OK, Content-Type: text/html [ENCRYPTED WITH AES-256-GCM]
If a network eavesdropper captures this encrypted data, they see only random-looking garbage.
Why This Design is Brilliant
ECC Key Exchange Agree on symmetric key securely | Speed - Moderate | Security - High
AES Encryption Encrypt bulk data | Speed - Very fast | Security - High
ECDSA Certificates Prove identity | Speed - Fast | Security - High
Ephemeral Keys Limit damage if long-term key compromised | Speed - - | Security - Forward secrecy
Forward Secrecy: Even if Amazon's long-term private key is compromised tomorrow, today's connections remain secret because they used ephemeral keys.
So, that's it for now, i'll be uploading another part for why these cryptographic algoriths are at risk now. Stay tuned.
So, that's it for now, i'll be uploading another part for why these cryptographic algoriths are at risk now. Stay tuned.
Read about Quantum Threats, Part II here:
flatline
I am a cybersecurity enthusiast and an ethical hacker who's passionate about technology, loves to learn and now here I am sharing what I've learned so far.
I have been tinkering around with these digital thingies for a long time. I have experience in Information Security, Computer & Network Administration, Operating Systems, Web Development, Programming, Graphic Designing, Video Editing and so on.
I've always been keen to know that how things work, most importantly how they break!!
